Zenão de Eléia é um lógico e filósofo grego que é conhecido principalmente pelos paradoxos mencionados em sua homenagem. Não se sabe muito sobre sua vida. A cidade natal de Zenão é Elea. Também nos escritos de Platão, foi mencionado o encontro do filósofo com Sócrates.
Por volta de 465 aC e Zenão escreveu um livro no qual esboçou todas as suas idéias. Mas, infelizmente, não chegou aos nossos dias. Segundo a lenda, o filósofo morreu em uma batalha com um tirano (presumivelmente o chefe de Elea Nearch). Todas as informações sobre Elea foram coletadas pouco a pouco: nas obras de Platão (nascido 60 anos depois, Zenão), Aristóteles e Diógenes Laertius, que escreveram três séculos depois um livro de biografias de filósofos gregos. Zenão também é mencionado nos escritos dos representantes posteriores da escola de filosofia grega: Themisty (século IV dC), Alexander Afrodinsky (século III dC), bem como Philoponus e Simplicius (ambos vividos no século VI dC).. Além disso, os dados nessas fontes são tão consistentes entre si que todas as idéias do filósofo podem ser reconstruídas a partir deles. Neste artigo, falaremos sobre os paradoxos de Zenão. Então, vamos começar.

Paradoxos do conjunto
Desde a era de Pitágoras, o espaço e o tempo eram considerados exclusivamente do ponto de vista da matemática. Ou seja, acreditava-se que eles eram compostos de muitos pontos e pontos. No entanto, eles têm uma propriedade que é mais fácil de perceber do que definir, a saber, “continuidade”. Alguns paradoxos de Zenão provam que ele não pode ser dividido em momentos ou pontos. O raciocínio do filósofo se resume ao seguinte: "Suponha que tenhamos concluído a divisão até o fim. Então, apenas uma das duas opções é verdadeira: obtemos as quantidades ou partes mínimas possíveis indivisíveis, mas infinitas em quantidade ou divisão nos levará a partes sem magnitude, uma vez que a continuidade, sendo homogênea, deve ser divisível em qualquer circunstância. Não pode ser divisível em uma parte, mas não na outra. Infelizmente, ambos os resultados são bastante ridículos. O primeiro se deve ao fato de que o processo de divisão não pode terminar enquanto houver partes no restante que tenham um valor. E a segunda é porque, em tal situação, inicialmente o todo seria formado do nada. ” Simplicius atribuiu esse argumento a Parmênides, mas é mais provável que seu autor seja Zenão. Nós vamos além.
Paradoxos de movimento de Zenão
Eles são considerados na maioria dos livros dedicados ao filósofo, porque entram em dissonância com evidências dos sentimentos dos eleaticos. Em relação ao movimento, distinguem-se os seguintes paradoxos de Zenão: "Flecha", "Dicotomia", "Aquiles" e "Fases". E eles vieram até nós graças a Aristóteles. Vamos dar uma olhada neles.
Arrow
Outro nome é o paradoxo quântico de Zenão. O filósofo afirma que qualquer coisa fica parada ou se move. Mas nada está em movimento se o espaço ocupado é igual a ele em comprimento. Em um determinado momento, a seta em movimento está em um só lugar. Portanto, ele não se move. Simplicius formulou esse paradoxo em forma abreviada: “Um objeto voador ocupa um lugar igual no espaço, mas o que ocupa um lugar igual no espaço não se move. Portanto, a flecha está em repouso. Femistius e Phelopon formularam opções semelhantes.
"Dicotomia"
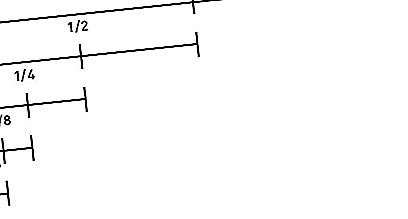
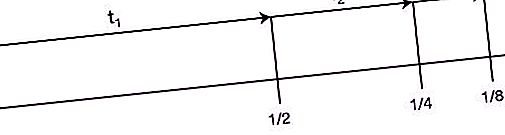
Toma o segundo lugar na lista de "Paradoxos de Zeno". É o seguinte: “Antes que um objeto que comece a se mover possa percorrer uma certa distância, ele deve superar metade desse caminho, depois metade do restante, etc., até o infinito. Como durante divisões repetidas da distância pela metade, o segmento se torna finito o tempo todo, e o número desses segmentos é infinito, essa distância não pode ser superada em um tempo finito. Além disso, esse argumento é verdadeiro tanto para pequenas distâncias quanto para altas velocidades. Portanto, qualquer movimento é impossível. Ou seja, o corredor nem será capaz de começar ".
Esse paradoxo comentou detalhadamente Simplicius, indicando que nesse caso um número infinito de toques deve ser feito em um tempo finito. "Qualquer pessoa que tocar em algo pode contar, mas o conjunto infinito não pode ser resolvido ou contado." Ou, como Philopon colocou, um conjunto infinito é indefinível.
Aquiles
Também conhecido como o paradoxo da tartaruga Zenão. Este é o argumento filosófico mais popular. Nesse paradoxo do movimento, Aquiles compete em uma corrida com uma tartaruga, que recebe uma pequena desvantagem no início. O paradoxo é que o guerreiro grego não conseguirá alcançar a tartaruga, já que primeiro ele alcançará o local de seu início, e ela já estará no próximo ponto. Ou seja, a tartaruga estará sempre à frente de Aquiles.
Esse paradoxo é muito semelhante a uma dicotomia, mas aqui a divisão infinita segue de acordo com a progressão. No caso de uma dicotomia, houve uma regressão. Por exemplo, o mesmo corredor não pode começar, porque ele não pode deixar sua localização. E na situação com Aquiles, mesmo que o corredor comece a se mover, ele ainda não virá correndo para lugar nenhum.
"Palco"
Se compararmos todos os paradoxos de Zenão em termos de complexidade, esse seria o vencedor. É mais difícil do que outros expor. Simplicius e Aristóteles descreveram esse raciocínio fragmentariamente, e não se pode confiar em sua confiabilidade com 100% de certeza. A reconstrução desse paradoxo tem a seguinte forma: sejam A1, A2, A3 e A4 corpos imóveis do mesmo tamanho, e B1, B2, B3 e B4 sejam corpos do mesmo tamanho que A. Os corpos B se movem para a direita, de modo que cada B passe E em um instante, que é o menor período de tempo possível. Seja B1, B2, B3 e B4 corpos idênticos a A e B e mova-se em relação a A para a esquerda, superando cada um dos corpos em um instante.
Obviamente, B1 superou todos os quatro corpos de B. Vamos levar para uma unidade o tempo que levou para um corpo de B passar por um corpo de B. Nesse caso, foram necessárias quatro unidades para todo o movimento. No entanto, acreditava-se que os dois momentos passados para esse movimento eram mínimos e, portanto, indivisíveis. Daqui resulta que quatro unidades indivisíveis são iguais a duas unidades indivisíveis.